概要

在纤维增强复合材料中，由于基体和增强体之间的交互载荷传递，即使在简单的外部载荷条件下，复合材料也表现出复杂的内部变形行为。复合材料构件在实际使用条件下通常会经历比简单单轴加载复杂得多的加载状态，因此必须使用计算方法来检查不同局部材料点处的多轴力学行为。2023年，《Composite Structures》期刊发表了由仁川国立大学机械工程系通过十字实验和有限元分析表征环氧聚合物的双轴压缩变形行为的研究工作。

本研究的目的是利用现有的十字型试样类型和测试方法，开发一种评估环氧聚合物初始屈服面的准确和系统的方法，并直接将所得表面与σ3=0平面第三象限的各种屈服函数进行比较。

试验材料与方法

        十字型试样由该研究团队自行制备完成，试样的几何形状参考了Smits等人的研究成果，加载臂采用向中心区域渐窄的过渡方法，中心区域进行铣削减薄处理。

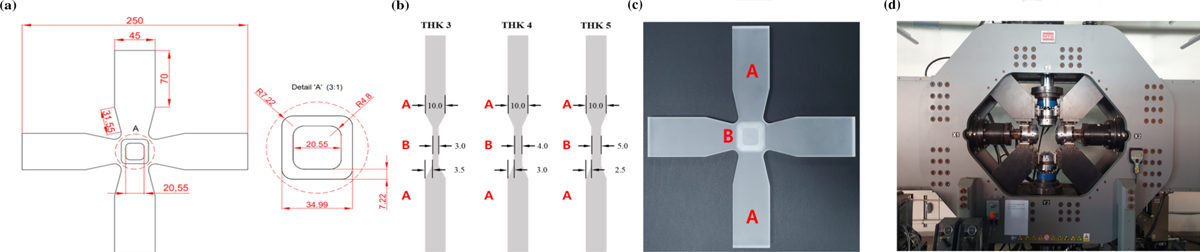
图 1 (a)十字型样品几何形状(俯视图)和(b)三种不同厚度的中心区域；(c)制备好的十字型标本；(d) MTS平面双轴和扭转试验系统(所有单位均为毫米)。

        该研究的重点是十字型试样双轴压缩加载路径下的变形行为，拟设定压缩载荷比为：-4:-10，-6:-10，-8:-10以及-10:-10，由于试样压缩会产生一定程度的屈曲，使用频率为2 Hz的激光距离跟踪器测量由于样品屈曲引起的测量区域的面外位移，以确定屈曲的开始(图2(a)和2(b))。 

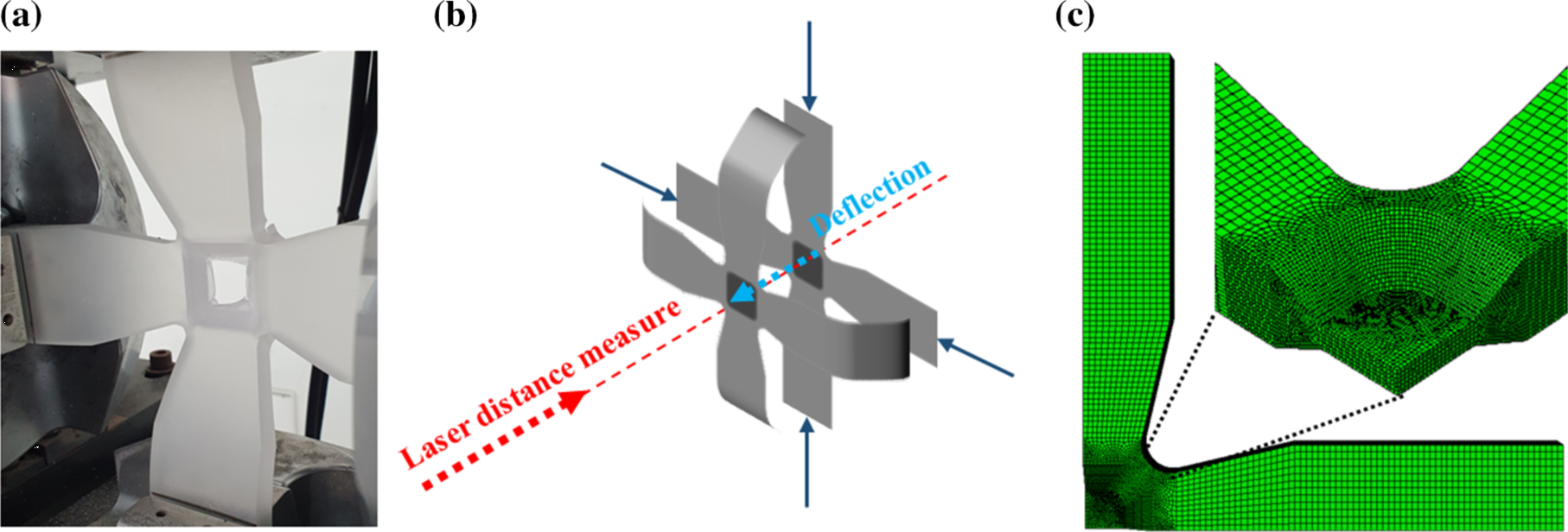
图 2 (a)通过双轴压缩载荷在中央标准区域破裂的弯曲十字形样品的图像；(b)使用激光距离跟踪器测量挠度的示意图；(c)十字形试件的四分之一有限元模型。

有限元分析

通过有限元建模分析，与一维变形试验不同，对于一些十字形几何形状的双轴试验，双轴应力状态不能从施加的载荷和测量区域的面积来计算。事实上，对于目前的试样几何形状，所施加的载荷不能完全转移到中心应变区，导致应变的估计值低于通过将所施加的载荷除以横截面积所确定的值，数值获得的应变区应力比通过简单地将施加的载荷除以横截面积获得的应力低大约35 %。

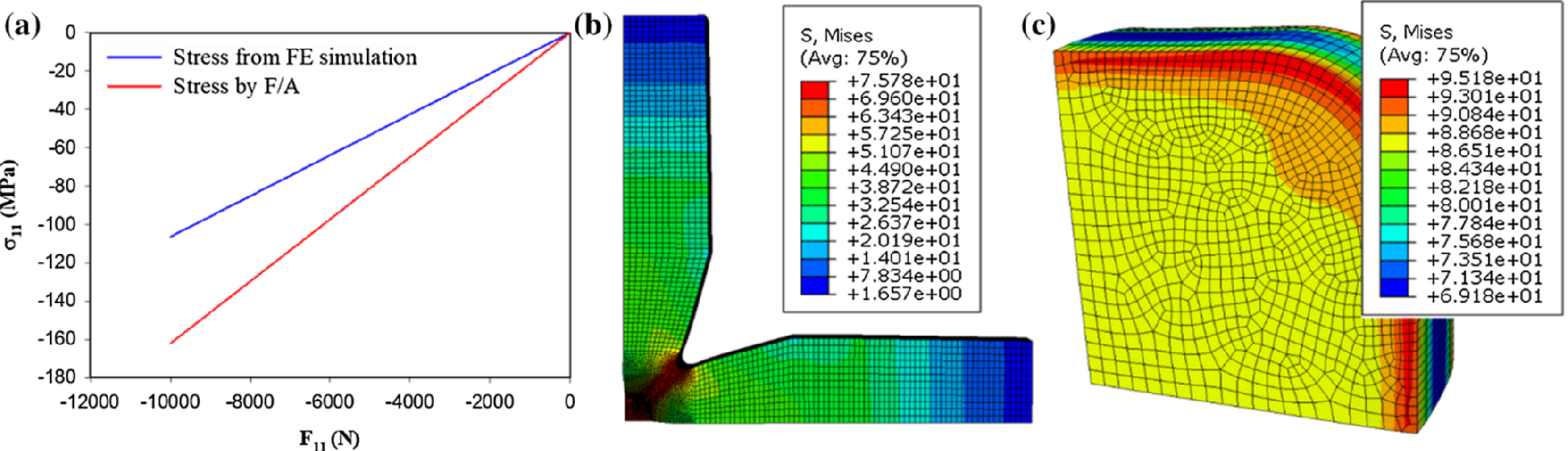
图 3 (a)分析结果和有限元结果的测量区域应力比较；(b)在等双轴压缩载荷下，整个十字形试样中的von Mises应力分布；(c)在等双轴压缩载荷下规范区域内的Von Mises应力分布。

        为了解决这个问题，多名研究人员建立与十字型样本的几何特征相对应的力-应力耦合关系，在面内应力状态下，应变区应力和施加的臂载荷之间的关系可以描述如下:

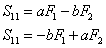
    a和b是描述耦合程度的常数，在考虑所有调查载荷比的弹性状态下，分别为13400-2和2800-2。同理，计量区域应变和加载臂施加位移之间也满足一定的线性转换定律即位移-应变耦合方程：

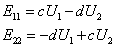
为评估屈曲位移对结果的影响，分别对三种不同中心厚度试样进行等载荷压缩，结果表明，更小中心厚度的试样的初始屈服更早，中心厚度与所承受载荷成正比，不会影响相应的位移。对于所有考虑的厚度比，试件在达到最大力后接近加载结束时发生屈曲。屈曲的发生与持续施加外载荷后应变软化机制引起的不稳定性有关。

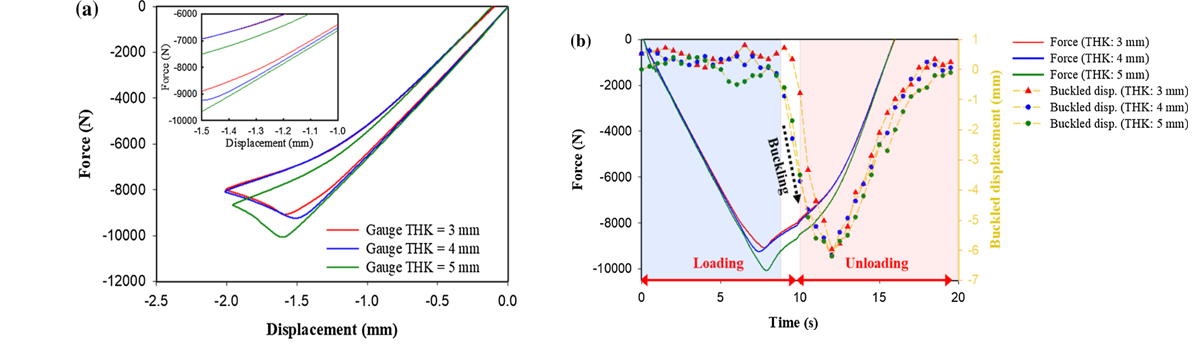
图 4 (a)不同规格区域厚度(3、4和5 mm)下的力-位移曲线及其(b)屈曲挠度曲线。

        从承受不同载荷比的十字形试件的双轴压缩试验中获得的力-位移曲线如图5所示。几乎所有的双轴分力剖面都表现出近乎线性的弹性变形、塑性硬化和软化状态，只有4:-10加载比除外，它表现为在更重加载的轴上力的大幅度连续增加，而在另一个轴上力的线性增加很小。

图 5 实验测得的力-位移曲线，负载比为:(a)-10:-10，(b)-8:-10，(c)-6:-10，(d)-4:-10。蓝点代表使用线性弹性材料定律的有限元模型获得的力-位移曲线；插图显示了确定屈服点附近的放大图。

基于偏移量的屈服准则

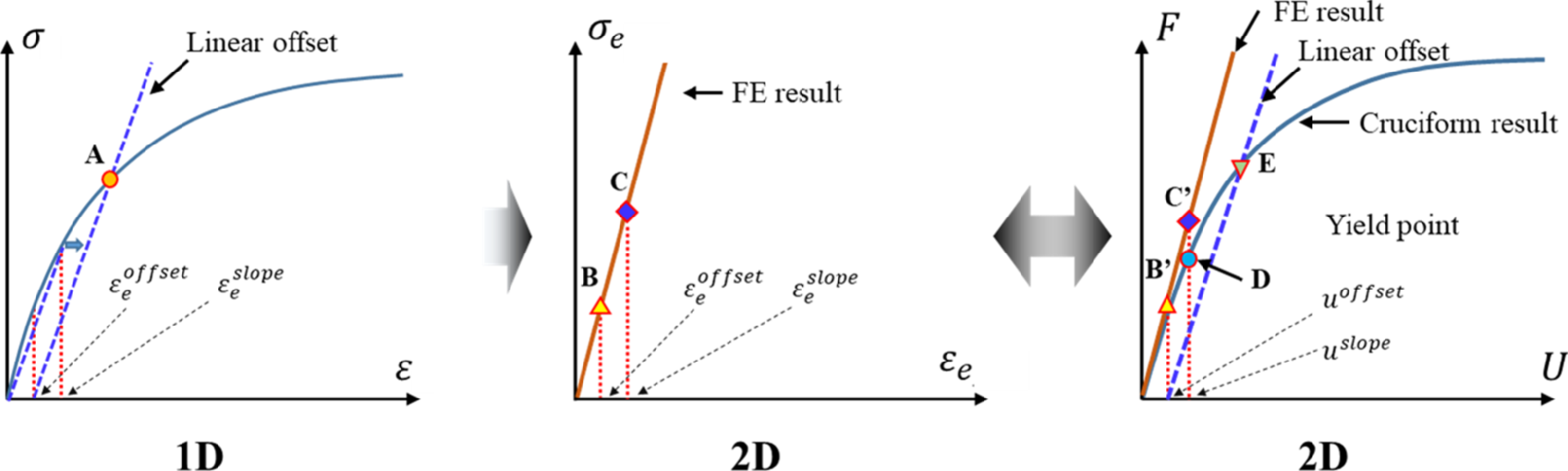
图 6 应用于双轴试验结果的基于偏移的屈服准则示意图

图6为所提出的屈服准则示意图，将偏移方法用于确定屈服点：

(1) 通过偏移线斜率、偏移应变和偏移应变范围确定一维屈服点A点；

(2) 使用线弹性材料模型根据的FE模拟的结果，确定中心规范区域中相应的有效应力和应变(B点和C点)；

(3) B点和C点的确定为图6中B '点和C '点在每个时刻通过位移-应变耦合方程估计每个加载臂的位移提供了基础；

(4) 从双轴试验结构画出线性偏移线，该线斜率为从零点到D点，通过得出的偏移位移与偏移位移范围确定此时的屈服点E；

(5) 最后通过力-应力耦合方程得出双轴屈服应力。

   文章接着说明了不同的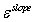和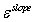对初始屈服面的影响，结果表明，随着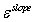的增加，由于偏移线斜率随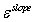的非线性衰减，所有考虑的载荷比的屈服面都略有扩大(如图7(a))。而当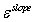增加到6e-4和7e-4时，试样屈服应力突然增加，增加的应力状态导致与光滑表面的相当大的偏差，并被判断为不太可能属于标准区域的适当屈服点(如图7(b))。

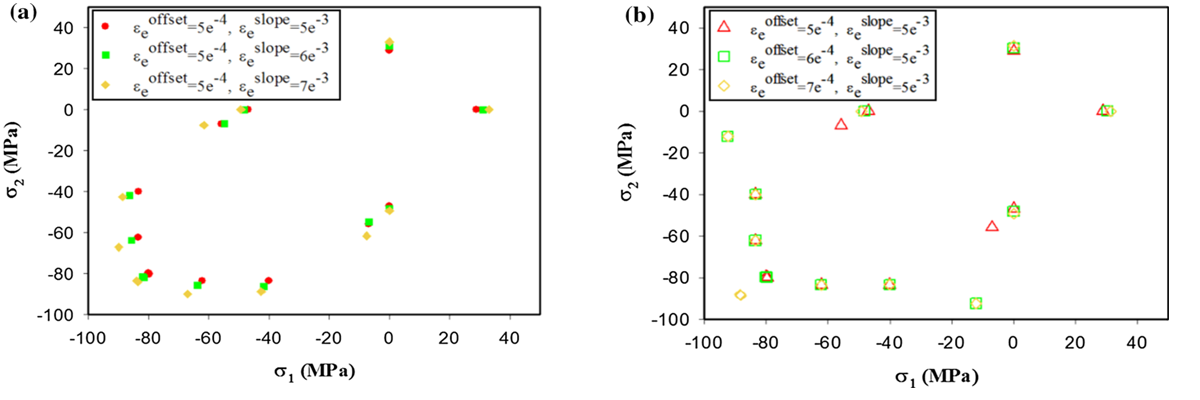
图 7 在不同偏移应变与偏移应变范围情况下基于偏移量的屈服准则情况

几种屈服准则对比

文章对比了抛物线、MD数据驱动和圆锥以及PMvM屈服函数之间的差别，结果表明，环氧聚合物的双轴压缩屈服响应偏离了抛物线和圆锥函数的预测，并且略小于MD数据驱动函数的预测(图8(a))，拟合的PMvM函数与双轴试验数据表现出相对较好的一致性(图8(b))，等双轴压应力和一维应力的比较表明，MD数据驱动和拟合的PMvM函数是环氧聚合物初始屈服面的合理选择(图8(c))。

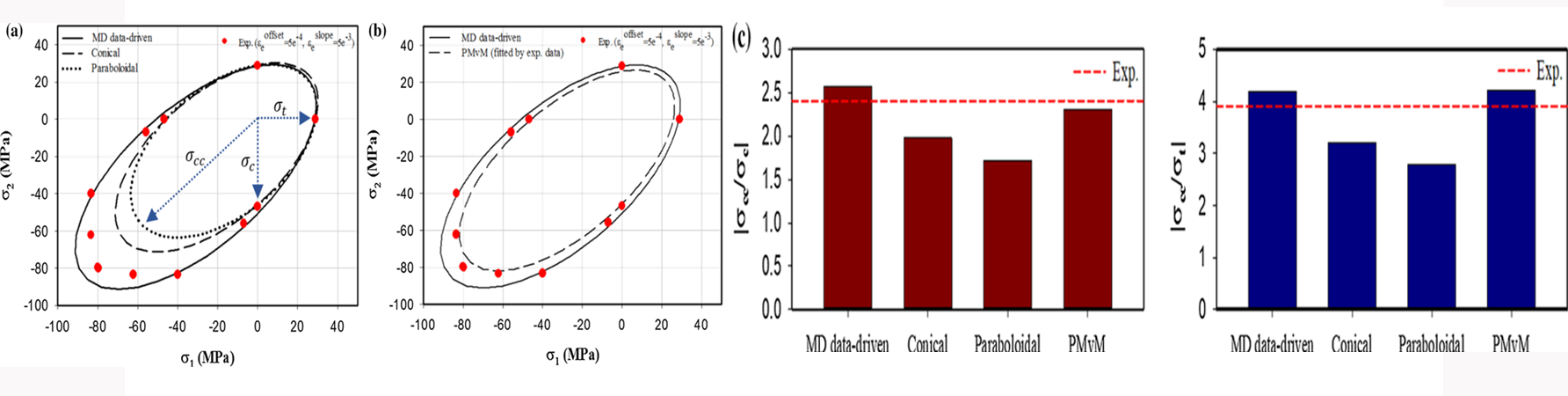
图 8 实验获得的屈服点与初始屈服面预测的比较(a)抛物线、圆锥和多维数据驱动的屈服函数，以及(b) PMvM和多维数据驱动的屈服函数获得的；(c)等双轴压缩应力大小与一维应力大小的比较

        使用基于抛物线和MD数据驱动屈服函数的材料塑性模型，在等双轴压缩载荷下进行了一系列有限元模拟。图9表明塑性变形的起点是试样拐角圆角处，并从此处扩展到中心测试区域，图9(b)的A、B、C、D分别代表试样开始塑性变形、中心区域开始塑性变形、中心区域塑性变形完全以及最大载荷试样变形状态。

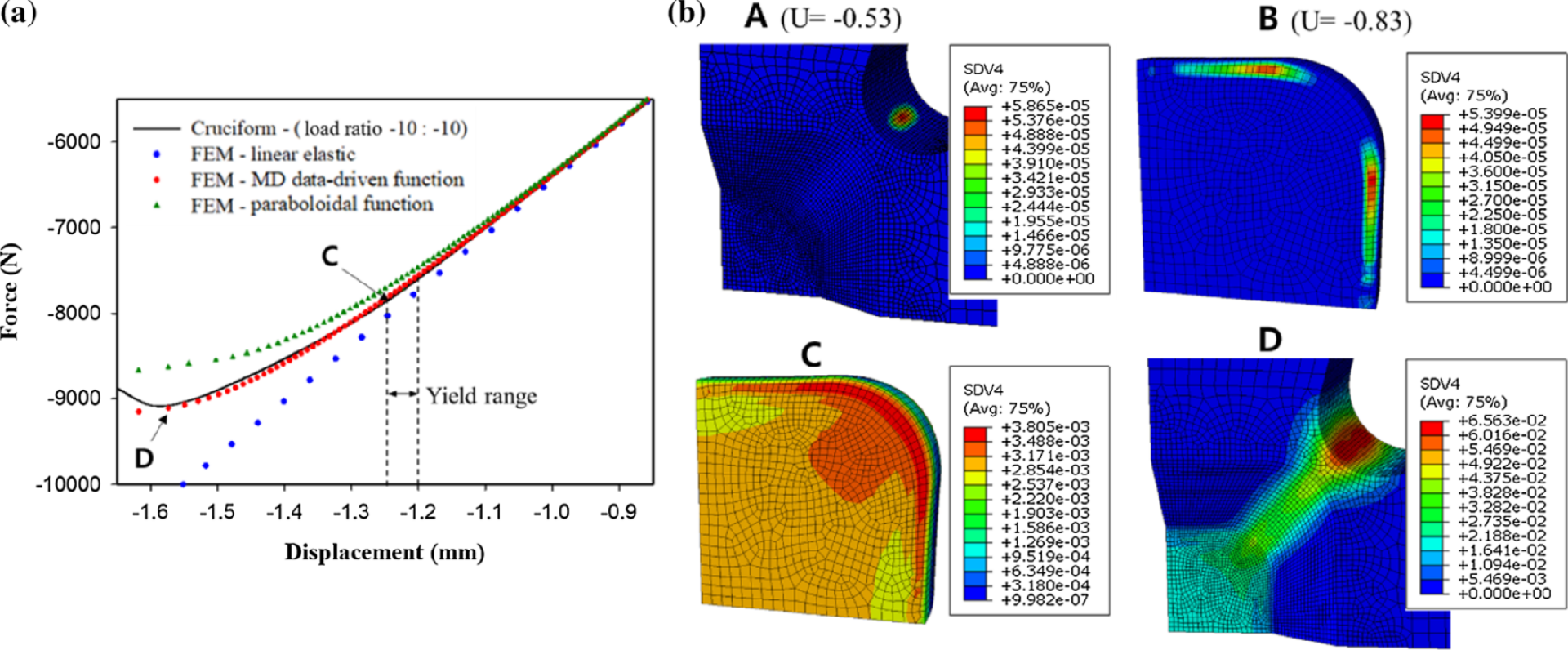
图 9 (a)等比加载双轴试验和有限元分析结果的力-位移曲线的比较,(b)不同位移条件下相应的等效塑性应变分布。(a)中的屈服范围代表由偏移屈服准则确定的位移范围；A和B分别表示在十字形试样和测量区域中第一次产生塑性变形的时间；C表示塑性变形在整个测量范围内完全发展；D表示试样在最大载荷下的变形

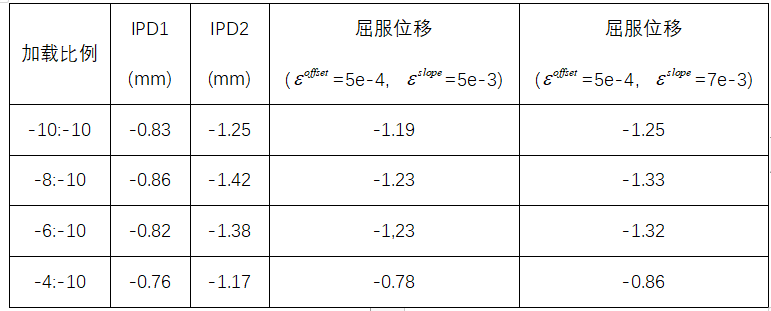
        使用从塑性变形的部分开始(IPD1)到完全发展的塑性变形(IPD2)的转变来识别中心测试区域的初始塑性变形。在等双轴压缩载荷下，将数值获得的IPD1和IPD2与在两种不同条件下(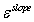=5e-4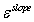，=5e-3)和(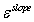=5e-4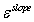，=7e-3)的屈服位移进行比较。加载比-4:- 10显示出比其他比值更低的IPD值，这与基于偏移量的屈服准则确定的屈服位移一致，这个结果可以解释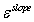为6e-4或7e-4的导致主应力分量的突变。

表 1 IPD与基于的偏移量的屈服准则确定的初始屈服位移对比(所示的IPD范围是基于MD数据驱动的产量函数获得的)

结论
        使用双轴测试和有限元分析对环氧树脂聚合物的初始屈服面进行了表征。据观察，在环氧树脂聚合物达到其最大应力状态之前，屈曲影响是可以忽略的。初始屈服面表现出广泛的应力状态，并没有被众所周知的抛物线或锥形屈服函数所描述。在双轴压缩载荷路径下，多轴屈服响应较慢，但更接近于由MD数据驱动的屈服函数所预测的。屈服后的等轴压缩行为由MD数据驱动的屈服函数更好地描述。然而，随着施加的载荷比偏离等轴条件，所有考虑的屈服函数越来越不能正确描述多轴变形反应。